Исторические и математические аспекты волнового принципа 

Леонард Фибоначчи Пизанский открыл числовую последовательность, названную в честь его имени, в XIII веке, но, если быть точным, данная последовательность была открыта еще до него. Для понимания данной математической последовательности стоит немного остановится на биографии самого Фибоначчи. В «народе» укрепилось словосочетание последовательность Фибоначчи, и с технической точки зрения это так и есть, данная цифровая цепочка, является последовательностью, а не рядом. В трактате Эллиотта «Закон природы», сам автор говорит, что основой его волнового принципа является математическая последовательность Фибоначчи. Если Вы хотите узнать больше о математической закономерности в волновом принципе, то советуем вам прочитать книгу Вальтера Е. Уайта «Математические основы волновой теории».

 

Леонардо Фибоначчи Пизанский

Период серьезного культурного упадка в Европе носит название «Темные Века». Этот период начался с краха Римской империи 476 года и продлился до 1000 года. В этот период многие науки в том числе и математика и философия претерпевали кризис в Европе, но вот в Индии и в странах арабского мира такое понятие как «Темные Века» не было, происходил наоборот расцвет наук. Благодаря развивающейся торговли и морскому пути через Средиземное море, Европа потихоньку стала выходить из состояния угасания. Коммерческие судна Индии и арабских стран приплывали в Европы и привозили с собой новые философские и математические познания и идеи, распространялась и культура других стран.

В период названным «ранее Средневековье» город-государство Пиза был замечательно процветающим местом, все это укрепляло его будущее развитие. Такие ценные для того периода товары как: хлопок и шерсть, кожа и мех, железо и медь и олово, различные заморские пряности покупались за стенами города-государства Пизы. В те времена главной валютой обмена между странами и континентами было конечно же золото. Порт Пизы весь был заполнен кораблями, которые весели не меньше четырех сотен тон и имели длину минимум восемьдесят фунтов. В самой Пизе занимались выделкой кожи, строили корабли и была развита обработка металлов. Политическая и экономическая жизнь в Пизе того времени была на высоком уровне развития даже по современным меркам. Пиза была республикой, в ней правили интересные законы. Например, главный магистрат города-государства за все время своей службы не получал жалования, а вот когда срок службы его истекал, тогда собирался консилиум, на котором проводили проверку его деятельности и в случае благополучных результатов работы, главный магистрат получал свою заработную плату за весь период работы. Неплохо, да? Леонардо Фибоначчи входил в состав такого консилиума.

Леонардо Фибоначчи Пизанский родился в период между 1170-1180 гг. Его отец был одним из городских чиновников и достаточно известным купцом. Есть предположения что вся семья жила в одной из башен Пизы. Башни могли быть сразу и крепостью, и мастерской и даже семейным домом. Все башни были построены так, что, если кто увидит чужака, который приходил с плохими намерениями, то этот кто-то мог выпустить в чужака стрелы, которые летели из крохотных и узких окон, а на голову врагу могли вылить кипящую смолу. По мнению историков, в то время, когда жил Фибоначчи, строилась легендарная падающая Пизанская башня, которая была колокольней.

В школьные годы Фибоначчи изучал таможенное дело и коммерческую практику тех времен. Все математические расчеты он делал с помощью абака. Это разновидность счетной доски, которая была довольна популярна в Европе тех времен и заменяла современный калькулятор. Абак в основном использовался для решения деловых задач. Леонардо Фибоначчи говорил на итальянском языке, но от также в совершенстве знал французский, греческий и латынь.

В период когда Леонардо Фибоначчи постигал науки, его отца назначили чиновником таможни в североафриканскую Боджию, и отец взял с собой Леонарда, чтобы мальчик закончил учебу. В то время Фибоначчи часто ездил с деловыми поручениями по Средиземному морю. Завершив одно из своих многочисленных странствий в Египет, Леонардо Фибоначчи публикует свое известное произведение под названием «Книга исчислений». В данном труде Леонардо рассказал европейцам о важнейшем математическом открытии за все время процветания наук, а именно о десятичной системе исчисления, о цифровом числовом ряде, где 0 был первой цифрой. В этой системе были представлены цифры, которые знакомы каждому современному первоклашке: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Этот цифровой ряд носит название индо-арабская система счисления, которой до сих пор пользуются большинство современных стран.

Эта индо-арабская система построена на разрядности числа. В системе любая величина характеризуется любым символом, который помещается в ряд с другими символами. Разрядность числа зависит и от номинальной величины, и от конкретного положения в ряду. Возьмем, например числа 25 и 52, оба эти числа имеют одинаковые символы, но различную величину. В истории это не первый пример изобретения системы исчисления. Математики Вавилона и индейцы майя никак не могли пересекаться, но обе эти цивилизации имели похожие системы исчисления на индо-арабскую, в которых были разряды, но метод древних жителей был очень сложен и неудобен. До появления индо-арабской системы исчисления, самая понятная система была вавилонская. Но она не была признана математическими системами Греции и Рима в виду своей сложности. Она включала семь символов, которые всем известны: I, V, X, L, C, D, M. С этими семью символами были связанны величины, которые не имели разрядов. Такие простые математические вычисления как умножение и деление, сложение и вычитание являлись очень сложными в этой системе, а особенно трудно было проводить вычисления на больших цифрах. И тут пригождалось нами уже упомянутое устройство «абака», для помощи в решении математических примеров с большими числами. Так как данный инструмент основан на принципе разрядности и использовал ноль, он был обязательным атрибутом в римской вычислительной системе. На протяжении сотни лет математики, купцы и бухгалтеры использовали его в качестве помощника, занимаясь вычислениями. После того как Фибоначчи выпустил свой трактат «Книга исчислений», он все время использовал именно индо-арабскую систему счисления во время всех своих странствий. Благодаря просветительской работе Фибоначчи, эта новая система прижилась в Европе и понравилась математикам своей простотой и легкостью исчислений. Арабские числа постепенно стали заменять римские цифры во всей Европе. Появление индо-арабской системы в европейском обществе считается важнейшим математическим достижением тех времен за целых семь столетий с момента распада Римской Империи. «Темным векам» пришел конец. Считается, что благодаря именно Леонарду Фибоначчи такая наука как математика смогла выжить в Европе в Средние века. Но также Фибоначчи смог заложить фундамент для великих математических открытий, а это способствовало развитию физики, инженерии и астрономии.

Фибоначчи легко можно назвать одним из величайшие людей своего времени. Он был своего рода знаменитостью в области науки и многие известные ученые, философы и исследователи приезжали в город-государство Пизу, чтобы лично познакомиться с Фибоначчи. Одним из таких людей был Фредерик II, император Священной Римской Империи Германских Наций, королем Сицилии и Иерусалима. Он был членом двух самых известных семей Европы и Сицилии (одно из влиятельнейших государств той эпохи. Фредерик II был ярым монархистом, предпочитал богатство и вел пышную жизнь. Встреча императора и Леонардо Фибоначчи состоялась примерно в 1225 году и это было особым событием для города-государства Пизы. Император Фредерик II привел с собой огромную процессию, в которой были и трубачи, и рыцари, и придворные, и чиновники, и даже различные звери из императорского парка. Многие задачи, которые были поставлены Фредериком II перед великим Леонардом Фибоначчи, были решены в исправленном трактате «Книга исчислений», а новое издание было посвящено Императору.

Сказать, что Леонардо Фибоначчи Пизанский был величайшим математиком средневековой Европы, это значит ничего не сказать. Он написал три величайших математических произведений: первое – это «Liber Abacci», первое издание данной книги вышло в 1202, а в 1228 свет увидел новое и дополненное издание книги, которая и была посвящена Императору; второе – это «Practica Geometriae», данная книга вышла в 1220 году; и третье произведение – это «Liber Quadratorium». Сохранился документ, дотированный 1240 годом, в котором жители современники Леонарда Фибоначчи, называют его «благоразумным и ученым мужем». А относительно недавно Джозеф Гайз, который являлся старшим редактором «Британской Энциклопедии» произнес, что в будущем исследователи будут величать Леонарда как главного в мире пионера мысли. Все работы Леонарда Фибоначчи Пизанского относительно недавно перевели с латинского на английский и далее на множество других языков. Если Вы хотите узнать подробнее о его работах, можете прочитать книгу Джозефа Гайза «Леонард Пизанский и новая математика Средних веков». Это произведение, повещенное жизни и трактатам Фибоначчи, и той эпохи, когда жил этот гений.

Бесспорно, Леонардо Фибоначчи Пизанский был один из величайших людей того времени. Но в наше время сохранилась лишь его статуя, которая находится в Пизе в современной Италии, и которая стоит рядом с великой Падающей Пизанской башни, на другом берегу реки Арно. Также в наше время есть две улицы, носящей имя гения, первая находится в самой Пизе, а вторая во Флоренции. Не многие современные жители знают имя Фибоначчи, особенно ярко это ощущается в Пизе. Огромное количество туристов ждут своей очереди, чтобы сфотографироваться с знаменитой падающей Пизанской башней, а вот место, где находится статуя Фибоначчи, не пользуется популярностью. Фибоначчи и Бонанн, архитектор, который спроектировал и построил Пизанскую башню, были современники. Два этих человека внесли большой вклад в историю, но Фибоначчи внес бесспорно больший вклад, но его имя не столь узнаваемо как имя Бонанны.

Последовательность Фибоначчи

В трактате Леонардо Фибоначчи Пизанского «Книга исчислений» определяется некоторая задача, из решения которой появляется закономерность чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1587, 2584 и так далее. Данная бесконечная числовая последовательность имеет название «Последовательность Фибоначчи». Задача, которая была сформирована в трактате «Книга исчислений» звучит так:

«Если в некое закрытое пространство поместить одну пару кроликов, то сколько таких пар получится за один год, при условии, что каждая пара кроликов производит новую пару каждый месяц, начиная со второго?»

Решая данную задачу, вначале следует заметить, что все пары кроликов (и первая в том числе) в первый месяц не приносят потомства, а вот начиная со второго месяца, она приносят на свет еще одну новую пару кроликов. Поэтому в начале второго месяца количество кроличьих пар не изменилось, их так же одна пара. И мы можем начать создавать последовательность Фибоначчи. Пока у нас 1, 1. Первая пара кроликов производит на свет еще одну пару кроликов во втором месяце, и у нас получается в самом начале третьего месяца две пары кроликов. Далее происходит следующее: в третьем месяце первая пара наших кроликов приносит на свет новую пару, третью пару кроликов, и в самом начале четвертого месяца у нас три пары кроликов. Наша последовательность Фибоначчи растет: 1, 1, 2, 3. В середине/конце месяца две первые пары кроликов разрастаются, давая опять потомство, а новая пара кроликов пока не приносит потомство, таким образом у нас пока пять пар кроликов. В новом месяце первые три пары кроликов производят на свет новые три пары, а две пары не приносит. Наша последовательность Фибоначчи снова растет: 1, 1, 2, 3, 5, 8. Ниже на рисунке 3-1 Вы можете видеть «Генеалогическое древо семьи Кроликов». Любой школьник, посмотрев на этот рисунок скажет, что кролики растут с экспоненциальным ускорением.

(Рис.3.1)

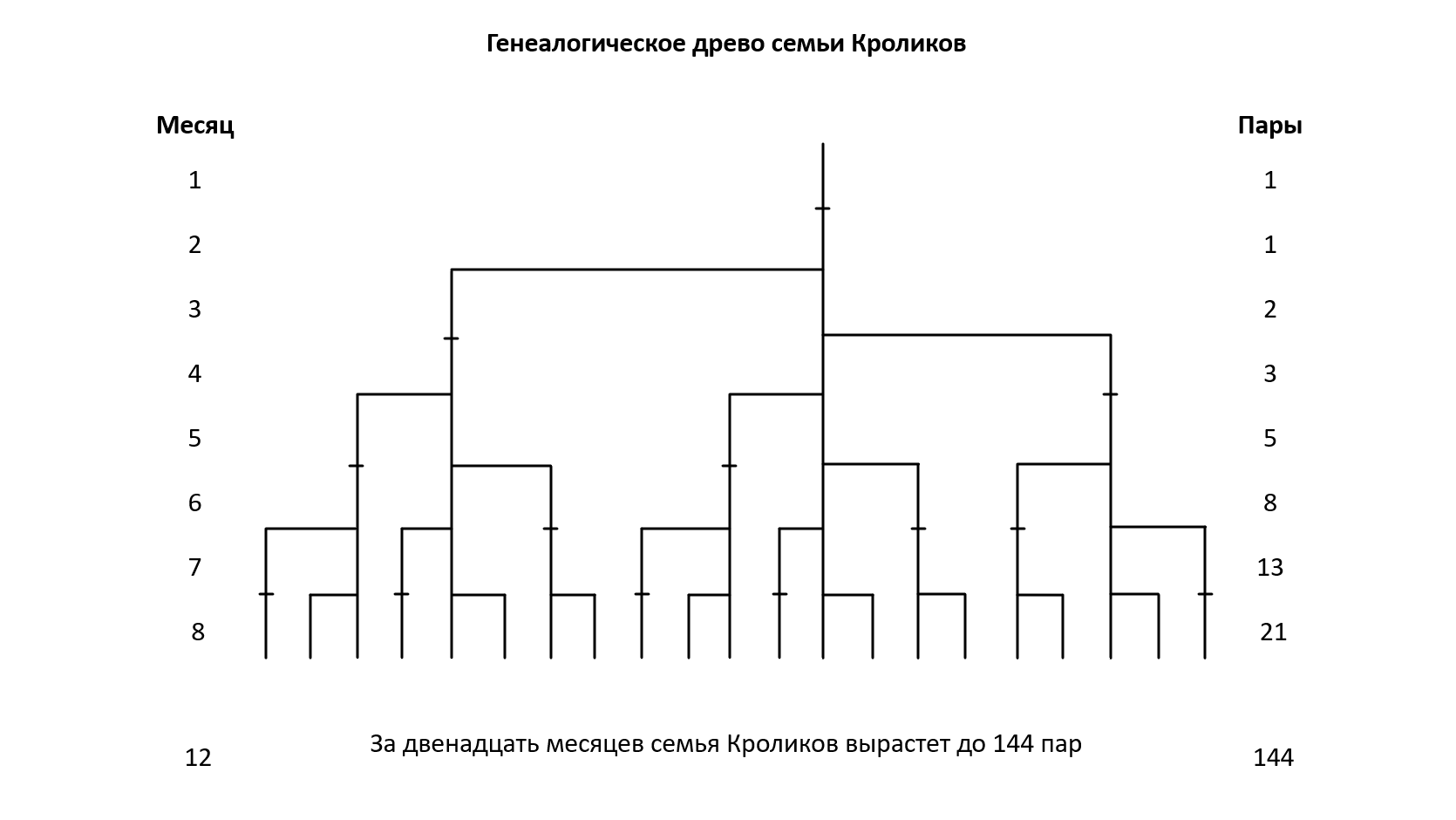
Если продолжать считать появление на свет пары кроликов в течении всего пары лет, то цифры будут колоссальными, астрономическими. Всего лишь через десять лет у нас бы так получилось, что мы бы имели 3544224848179261915075 пар наших кроликов. Кажется, что всего на всего мы решаем задачу с кроликами, поставленную в трактате Фибоначчи, но данная выявленная закономерность обладает многими необычными свойствами. Например, если вы захотите посчитать отношение между членами этой последовательности, которые находятся на одном и том же расстоянии от друг друга, то вы найдете, что это самое отношение почти неизменно.

Леонардо Фибоначчи вывел, что если взять и сложить два любых соседних числа, то получится число, идущее сразу за вторым числом, играющим в сложение. Например, рассмотрим самое начало последовательности Фибоначчи 1, 1, 2, 3, 5, 8 (1+1=2; 1+2=3; 2+3=5; 3+5=8 и так вплоть до бесконечности).

Золотое соотношение

Вот еще одно магическое свойство последовательности Фибоначчи: если не брать в расчет несколько первичных цифр в последовательности, то можно увидеть, что отношение любого числа к следующему идущему числу равно примерно 0,618, а ко второму идущему числу 1,618. Также нужно заметить, чем порядковый номер члена последовательности является больше, тем ближе его соотношение к числу «фи». Число «фи» считается иррациональным числом, оно примерно равно 0,618034…. А вот если взять соотношения между членами последовательности Фибоначчи, разделенными только одним числом, то мы заметим, что у нас получилось значение около 0,382. А если рассмотреть обратное отношение двух чисел, разделенных одним числом, то мы заметим, что у нас получилось значение около 2,618. Ниже на рисунке 3-2 вы можете видеть таблицу, в которой изображается отношение чисел последовательности Фибоначчи от 1 и до 144.

(Рис.3.2)

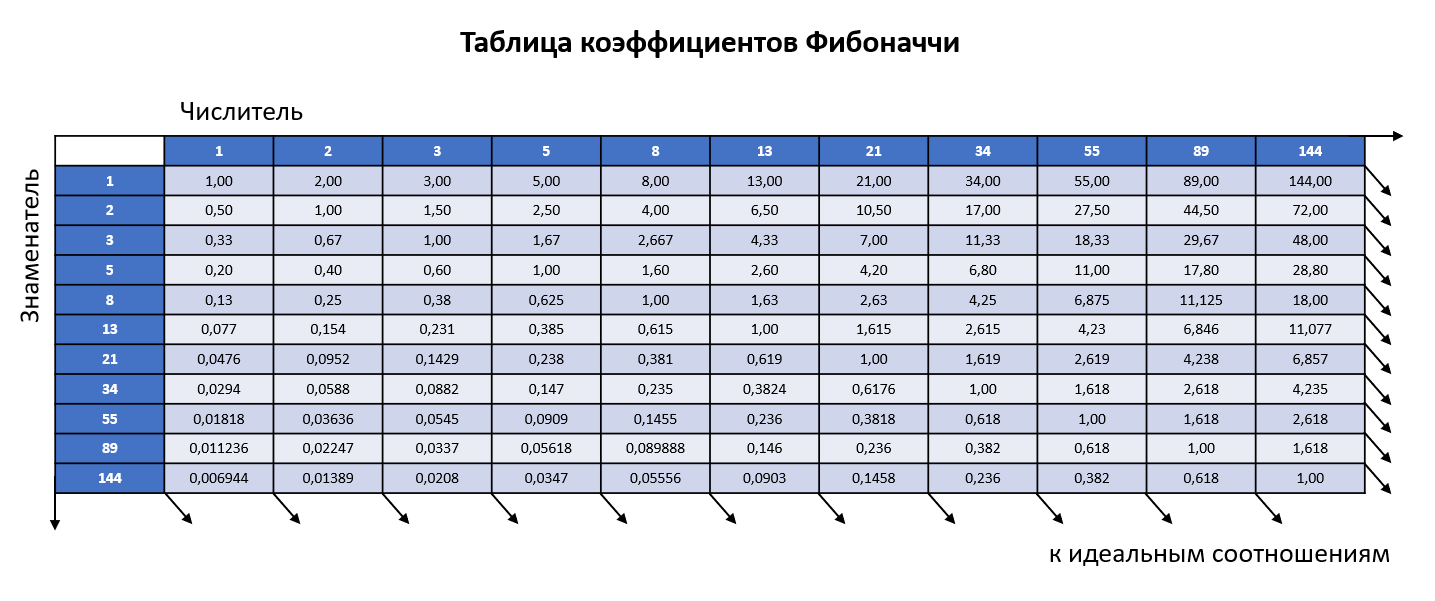
Число «фи» это одно единственное число в математике, к которому можно прибавить число один и получить обратное себе число:

 1 + 0,618 = 1 : 0,618

 

Эта закономерность сложения и умножения наводит нас на новую последовательность уравнений:

 0,618² = 1 – 0,618

 0,618³= 0,618 – 0,618²

 0,618⁴ = 0,618² – 0,618³

 0,618⁵ = 0,618³ – 0,618⁴

 или

 1,618² = 1 + 0,618

 1,618³ = 1,618 + 0,618²

 1,618⁴ = 1,618² + 0,618³

 1,618⁵ = 1,618³ + 0,618⁴

 

Также у этих четырех коэффициентов есть интересные взаимодополняющие свойства, они представлены ниже:

 1,618 – 0,618 = 1

 1,618 * 0,618 = 1

 1 – 0,618 = 0,382

 0,618 * 0,618 = 0,382

 2,618 – 1,618 = 1

 2,618 * 0,382 = 1

 2,618 * 0,618 = 1,618

 1,618 * 1,618 = 2,618

 

Также у последовательности Фибоначчи есть и другое интересное свойство. Вы можете взять абсолютно любое число из последовательности (исключая только числа 1 и 2), и помножить эти числа на 4, а затем сложить с определенным числом из последовательности, у вас выйдет другое число последовательности. Например:

 3 * 4 = 12       12 + 1 = 13

 5 * 4 = 20       20 + 1 = 21

 8 * 4 = 32       32 + 2 = 34

 13 * 4 = 52     52 + 3 = 55

 21 * 4 = 84     84 + 5 = 89

 и так далее.

 

Мы видим, что по мере увеличения роста новой прогрессии в последовательности, цифры формируют новую уже третью закономерность, которая составлена из цифр, к которым нужно прибавить произведения четверки и прибавить число Фибоначчи. Эта закономерность является сформированной, потому что взаимоотношения членов в последовательности Фибоначчи относятся друг от друга ровно на 2 позиции и являются равным 4,236. При этом значение 0,236 есть обратное число к 4,236, а еще по мимо всего это формирует разность в числах 4,236 и 4.

Также Вы можете ознакомиться с несколькими вторичными закономерностями, которые последовательность Фибоначчи образует.

1) Ни одни из любых 2 закономерностей чисел Фибоначчи не составляют общих делителей.

2) Можно пронумеровать все цифры в данной закономерности (за исключением числа 3, которое является четвертым номером в последовательности Фибоначчи – 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее) №1; №2; №3; №4; №5; №6; №7; №8; №9 и так далее, мы можем заметить, что № абсолютно каждого из чисел в последовательности Фибоначчи оказывающимся простым числом и есть простое число. Просто число — это натуральное число, которое больше единицы, и у которого есть всего два делителя, а именно единица и само это данное число. И также похожим образом, (за исключением числа 3, которое является четвертым номером в последовательности Фибоначчи – 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее), все остальные составные № чисел последовательности Фибоначчи являются соответствием составных цифр Фибоначчи ( это иллюстрирует таблица ниже). А вот противоположное, не каждый раз оказывается правильным. Составное число – это такое натуральное число, которое имеет более двух делителей, кроме единицы и самого себя.

3) Если взять любые чисел из последовательности Фибоначчи и их все сложить, то мы заметим, что вся эта сумма делится на одиннадцать без остатка.

4) Если сложить все числа в последовательности Фибоначчи до одной определенной цифры в последовательности и прибавить число один, то мы получим число равное определенному числу в последовательности Фибоначчи, которое отстаёт ровно на два числа от того числа, которое было прибавлено последним.

5) Если сложить сумму квадратов любых последовательных членов в последовательности Фибоначчи, которая бы начиналась с первой, то мы получим что данная сумма будет равняться крайнему числу в данной закономерности и которое умножили на следующий стоящий член. Число должно быть из данной выборки.

6) Если взять квадрат любого числа из последовательности Фибоначчи и вычесть из него квадрат второго члена последовательности Фибоначчи (считаем в сторону уменьшения), получится всегда одно из чисел последовательности Фибоначчи.

7) Если взять квадрат любого числа из последовательности Фибоначчи и умножить его на следующее стоящее после него число из последовательности Фибоначчи, то получится число равное предыдущему члену в последовательности Фибоначчи (но значение может оказаться с погрешностью – плюс минус единица). В данном примере вычитание и сложение единицы чередуется относительно развития последовательности Фибоначчи.

8) Если взять и сложить квадрат числа F_n с квадратом следующего числа их последовательности Фибоначчи, то есть F_n+1, то получится значение равное числу Фибоначчи в соотношении F_2n+1. Получается форма уравнения: F_n² + F_n+1 ² =  F_2n+1. Данная формула используется в простых прямоугольных треугольниках. Ведь в них если сложить значение двух коротких сторон, то получится квадрат равный третьей самой длинной стороны. Ниже вы можете увидеть иллюстрацию, к которой применяется F₅ и F₆ и корень квадратный из F₁₁.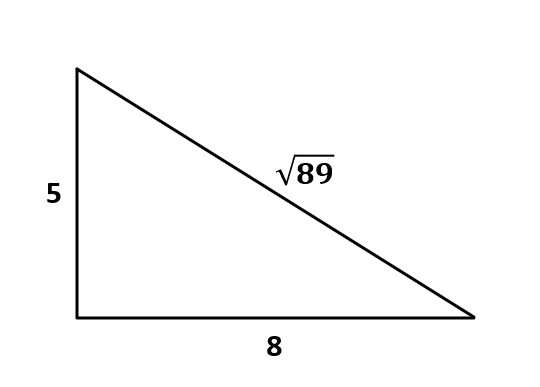

9) В математики существует формула, которая помогает выявить отношения двух самых часто встречающихся «иррациональных чисел» «φ» и «π»:

F_n = 100 * π² * φ^(15-n)

где:

• «φ» = 0,618…,
• «π» является порядковым номером в данной последовательности,
• «F_n» является непосредственно самим членом этой последовательности.»

В этом конкретном примере число «1» является только однажды и получается, что: F₁ ≈ 1; F₂ ≈ 2; F_{3 ≈} 3 и так далее.

Пример:

если, n =7, то: F₇ ≈ 100 * 3,1416₂ * 0,6180339^(15-7) ≈ 986,97 * 6180336⁸ ≈986,97 * 0,021129 ≈ 21,01 ≈ 21.

10) Еще одно «магическое свойство» в последовательности Фибоначчи, о котором мы еще не упоминали заключается в том, что все соотношения между числами в последовательности равны числам, которые достаточно схожи с тысячными долями других чисел в последовательности, но при погрешности, которая равна всего лишь тысячной доли другого числа последовательности.

• Если мы рассматриваем отношения между числами в последовательности Фибоначчи в сторону увеличения двух почти одинаковых чисел Фибоначчи, мы получаем значение равное единицы (либо как 0,987 + 0,013 = 1);
• Соседствующие числа в последовательности относятся друг к другу как 1,618 (либо как 1,597 + 0,021 = 1);
• Если взять некое число в последовательности Фибоначчи и выявить отношения между его правым ближайшим «соседом» и левым ближайшим «соседом», то у нас получится значение равное 2,618 (либо как 2,584 + 0,034 = 2,618) и так далее.
• Если мы хотим рассмотреть обратное отношения одного соседнего числа к другому в последовательности Фибоначчи, то мы увидим значения равное 0,618 (либо как 0,610 + 0,008 = 0,618);
• Если взять некое число в последовательности Фибоначчи и выявить обратное отношения между его правым ближайшим «соседом» и левым ближайшим «соседом», то у нас получится значение равное 0,382 (либо как 0,377 + 0,005 = 0,382);
• Если мы возьмем некое число последовательности Фибоначчи, а между данным числом будет находится два члена последовательности Фибоначчи, то у нас получится отношение равное значению 0,236 (либо как 0,233 + 0,003 = 0,236);
• Если мы возьмем некое число последовательности Фибоначчи, а между данным числом будет находится уже три члена последовательности Фибоначчи, то у нас получится отношение равное значению 0,146 (либо как 0,144 + 0,002 = 0,146);
• Если мы возьмем некое число последовательности Фибоначчи, а между данным числом будет находится уже четыре члена последовательности Фибоначчи, то у нас получится отношение равное значению 0,090 (либо как 0,089 + 0,001 = 0,090);
• Если мы возьмем некое число последовательности Фибоначчи, а между данным числом будет находится уже пять членов последовательности Фибоначчи, то у нас получится отношение равное значению 0,056 (либо как 0,055 + 0,001);
• Если мы возьмем некое число последовательности Фибоначчи, а между данным числом будет находится уже от шести до двенадцати членов последовательности Фибоначчи, то у нас получится отношения равные значениям, которые и являются сами тысячными долями чисел в последовательности Фибоначчи, начиная с 0,034.

Необычно то, что в данных примерах, если проанализировать коэффициент, который связывает числа последовательности, между которыми находятся именно 13 членов числа Фибоначчи, то мы получим новый ряд чисел начиная с числа 0,001 и именно с тысячной доли того числа, где он начинался. При всех прочих подсчётах мы также получим схожесть или другими словами «само воссоздание в бесконечном ряду». И это само воссоздание показывает нам свойства «очень сильной связи среди практически всех отношений в математике».

И в последний момент мы хотим обратить ваше внимание на то, что:

(√5 + 1) / 2 = 1,618;

(√5 – 1) / 2 = 0,618,

где:

√5 = 2,236.

5 является одним из самых значимых чисел в волновом принципе Эллиотта, а сам квадратный корень этого числа и есть «ключ» к числу φ.

Само число 1,618 (или 0,618) называется в мире математики «золотым отношением» или же «золотым средним». Считается, что связанная с ним «идеальность» максимальна радует человеческое зрение и людской слух. Данное «золотое отношения» с древних времен подсознательно использовалось человеком в разных сферах и в науке, и в биологии, да и в музыке и живописи, и в архитектуре. В декабре 1975 году вышла статья Вильяма Хоффера в периодике, называемой «Smithsonian Magazine». В ней автор говорит следующее:

«Взаимоотношение между числами 0,618034 и 1 считается математическим фундаментом, формирующим основу формы карточной колоды и Парфенона. Это отношение встречается в нашей жизни довольно часто в подсолнухе и в морской раковине, его можно видеть в греческих вазах, и оно даже есть в «спиральной галактике внешнего космоса». В формировании множества произведений искусств неосознанно задействовано это отношение, и вся выдающаяся архитектура Греции имеет тоже пропорцию этого отношения. Древние греки, когда выявили закономерность данного отношение дали ей название, прозвав – «золотая середина».

Последовательность, которую вывел Фибоначчи, благодаря его знаменитым парам кроликов можно увидеть в самых необычных примерах. Последовательность чисел — это какая та «волшебная» закономерность, созданная самой природой, видимо поэтому она так приятна выглядит и звучит, и в целом приносит ощущение гармонии. Например, почти каждый человек знает, что вся музыка имеет в своей основе октавы в восемь нот. А вот если посмотреть на фортепиано, мы увидим, что оно состоит из восьми белых и пяти черных клавиш, что в сумме дает нам число тринадцать. Все музыканты знают, что для нашего уха нет большего наслаждения чем прослушивание музыкального интервала, который имеет название «секста». Интересно что в музыке нота «ми» имеет вибрации по отношении к ноте «до» в значении 0,62500, а это число незначительно отстает от нормы «золотой середины» все го лишь на 0,006966 пунктов. Данный музыкальны интервал «секста» доносится до нашего уха и передает вибрации «улитке среднего уха», а этот орган человеческого восприятия по «магической» случайности имеет форму логарифмической спирали.

В нашей природе с заведомой частотой встречается последовательность Фибоначчи и «золотая спираль». Данное частое появление может нам показать, почему это взаимоотношение числа 0,618034 к единице так нам приятно в искусстве, живописи и музыке. В искусстве и живописи и музыке человек воспроизводит то, что он видит и понимает в реальной жизни, а природа/реальная жизнь имеет в своей основе принципы «золотой середины».

Сама природа берет в основу правило «золотого отношения» и формирует с помощью него свои самые сложные и идеальные явления как микроизвилины мозга и молекулы ДНК, и даже такие огромные творения как целые галактики.

Природа, также опираясь на правило «золотого отношения» творит и создает такие явления как рост кристаллов, формирование мозга и даже нервной системы, преломление светового луча в стекле, структуру формирования всего живого (и растений и животных), музыкальные природные композиции. Ученые исследуют природные явления и творения и все больше убеждаются, что сама природа для себя создала принцип пропорциональности. Также посмотрев сейчас на свою руку, вы можете увидеть, что она состоит из пяти пальцев, а каждый палец в свою очередь состоит из трех частей. Получается, что в каждой руке есть отдельных 5 единиц, а каждая из этих пяти единиц делится на 3 и у нас получается закономерность 5-3-5-3, а данная прогрессия лежит в основе волнового принципа Эллиотта.

Золотое сечение

Любой математик скажет вам, что каждый отрезок можно разделить на несколько отрезков таким образом, что меньшая часть отрезка будет относиться к большей части отрезка так же, как и большая часть отрезка относится ко всему отрезку в целом. По «магической» случайности это соотношение будет равно 0,618.

(Рис.3.3)

Такое соотношение называется «золотым сечением», оно встречается в природе с заведомой регулярностью. Наше с вами тело во многих аспектах принимает принцип «золотого сечения», самое яркое проявление — это то, как построено наше лицо и как «идеально» одна его часть соотносится с другой частью, также яркий пример — это соотношения размеров нашего тела к размерам соотношений частей нашего тела. Также яркими природными примерами «золотого сечения» являются морские раковины и ракушки, рога животных, морские волны, сосновые шишки и семеня в подсолнечнике, соотношения молекул ДНК, формирование ураганов и водоворотов, и спиральная галактика. А самый яркий и древний пример рукотворного принципа «золотого сечения» является возведенный человеком храм Парфенон.

Питер Томпкинс заявляет, что Платон в своем трактате «Тимея» высказался очень сильно, он, рассматривая число φ, увидел принцип «золотого сечения» назвал его вездесущей математической закономерностью и произнес, что «золотое сечение» таит в себе ключ ко всем загадкам космоса. А в шестнадцатом веке Иоганн Кеплер произнес (имея ввиду принцип «золотого сечения» или как его еще называли тогда «Божественное сечение») мысль, что это сечение может описать все когда-либо созданное ведь оно показывает, что ко всем творением приложил руку Бог, создавая все по «своему подобию». Пулок изучая пропорции человеческого тела, разделяет его по принципу «золотого/Божественного сечения», но допускает небольшую погрешность в формировании и пользуется статистическим усреднением используя число максимально равное 0,618. При этом он также замечает, что и женское и мужское тело имеет в своем формирования принципы «золотого сечения», ведь оба тела были созданы «по подобию Бога». А в философии есть один интересный вопрос, который звучит так: является ли и прогресс человечества творением «по своему подобию?».

Золотой прямоугольник

Возможно, некоторые из вас помнят с уроков геометрии такое понятие как «золотой прямоугольник», это такой прямоугольник, в котором стороны имеют отношения 1,618 к 1. Чтобы лучше понять или вспомнить такой термин, предлагаем Вам самим построить данную фигуру. Для начала возьмите лист бумаги и нарисуйте квадрат, в котором все стороны были бы равны двум. Потом основание квадрата разделите на два одинаковых отрезка и поставите точку, от этой точки проведите прямую линию, которая бы соединяла самый верхний правый угол квадрата с данной точкой. Сделайте все так, как показано на иллюстрации ниже.

(Рис.3.4)

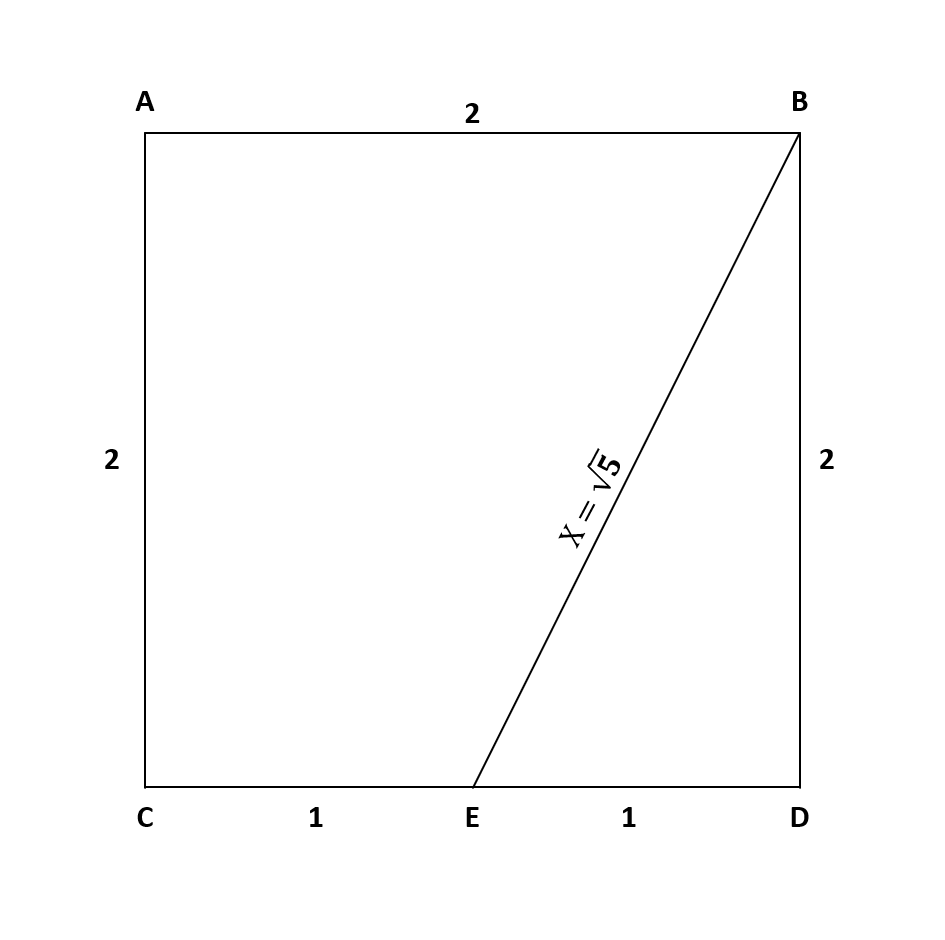
Проведя вершину, у нас получился треугольник, назовем его EDB, и он является прямоугольным. Около 550 года до Рождества Христова жил Пифагор и он доказал всеми известную теорему. Каждый старшеклассник знает, что квадрат гипотенузы в прямоугольном треугольнике равен сумме двух других его сторон (сумме катетов). Наша вершина и есть гипотенуза и назовем ее «Х». Таким образом у нас получается уравнение:

Х² = 2² + 1²      или      Х² = 5

А длинна нашей образующей (гипотенузы) ЕВ должна быть квадратным корнем из пяти – √5. Далее продолжим строить наш «золотой прямоугольник». Чтобы это сделать нам необходимо продлить основание квадрата или отрезка СD, и построить на нем новый отрезок ЕG, который должен быть равен квадратному корню из пяти – √5 или еще как в нашем случае он будет равен значению 2,236 единиц от длинны. Следуйте иллюстрации, приведенной ниже.

(Рис.3.5)

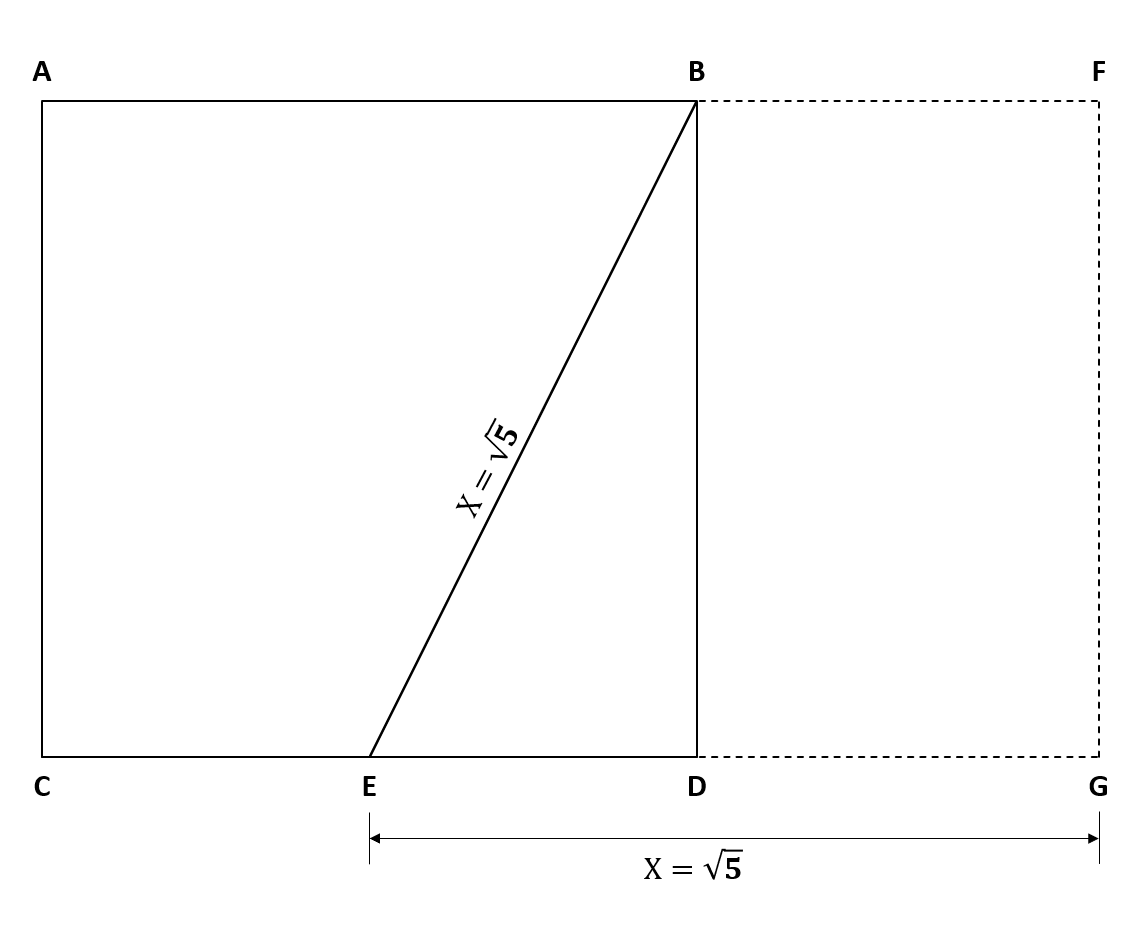
У нас получилось построить «золотой прямоугольник», стороны которого связанны «золотым коэффициентом». А самое интересное это то, что у нас получилось целых два «золотых прямоугольника» – первый AFGC, второй – BFGD. Это можно математически доказать

CG = √5 + 1

FG = 2

CG/FG = (√5 + 1)/2 = (2.236+1)/2 = (3.236)/2 = 1.618

 

DG = √5 – 1

FG = 2

DG/FG = (√5 – 1)/2 = (2.236-1)/2 = (1.236)/2 = 0.618

 

Мы доказали, что стороны во всех двух прямоугольниках связанны «золотым отношением», а значит эти два прямоугольника и сами являются «золотыми прямоугольниками» по определению.

Доказано, что если использовать «золотые прямоугольники» допустим в произведениях искусства, то для человеческого глаза они кажутся максимально привлекательными и гармоничными. Древние египтяне и греки знали этот прием и любили его часто использовать в искусстве в архитектуре. Интересно то, каким образом древние люди стали впервые использовать правило «золотого сечения» или принцип построения «золотых прямоугольников», знали ли они об этом, когда строили, производили ли замеры до строительства, или первые объекты были построены случайно? Также художники и архитекторы и скульпторы в период Ренессанса тоже любили использовать правила «золотого сечения». А в прочем во всех моментах развития человеческой цивилизации прослеживается это правило построения. Известно, что сам Леонардо да Винчи очень любил «золотое сечение» и в своих работах часто на него опирался. Он сам для себя считал красивым все что придерживается этого принципа, и даже говорил, что если вещь выглядит неправильно, то она не работает. Многие из его работ выглядят идеально, ведь при их создании он целенаправленно использовал методы «золотого сечения» и «золотого прямоугольника», чтобы добиться максимального усиления идеальности и привлекательности. Даже античные творцы использовали данный принцип, мы знаем, что Парфенон строился, придерживаясь принципу «золотого прямоугольника». В наше время современные скульпторы, художники и архитекторы тоже применяют это правило при создание своих работ. Зеркала, картинные и портретные рамы, окна, многие здания, кладбищенские кресты, книги — это все чаще всего создается, опираясь на правила максимального приближения к нормам «золотого прямоугольника».

Ученым совершенно понятно, что на всех людей, которые видят пропорции, связанные с числом φ, с правилом «золотого сечения» и с правилами построения «золотого прямоугольника», оказывается сильнейшее «культурное» воздействие. Ученые выявили, что мы думаем, что формы и пропорции, связанные с числом φ для нас, являются максимально эстетически привлекательными. Ученые много раз проводили эксперименты, например: они предлагали людям посмотреть на множество групп прямоугольников и выбрать только один. Намного чаще люди выбирали прямоугольники, построенные на пропорциях, связанных с числом φ. Также ученые предлагали людям поделить произвольно различные отрезки, и люди не задумывались делили их намного чаще так, как получается «золотое соотношение», причем люди делали это, не опираясь на знания о пропорции, связанной с числом φ.

Надо еще добавить, что в случае построения «золотого прямоугольника», так же, как и при построении объектов, основанных на правиле «золотого сечения», творцы опираются не только на эстетические моменты, но и удовлетворяют свои функциональные задачи. Для нас кажется наиболее не вероятный и функциональный пример построения согласно правилам «золотого прямоугольника», является формирование двойной спирали ДНК, ведь она сама создает максимально точные «золотые прямоугольники», изгибаясь в точности с правильными интервалами.

Мы может с большой долей уверенности сказать, что все творения, созданные на основе правила «золотого сечения» и правил построения «золотого прямоугольника», являются для человеческого глаза высшим эстетическим удовольствием, а также такие творения имеют максимально функциональное предназначение. А вот максимально сильным представителем эстетически несравненного динамизма, упорядоченного роста или прогресса можно считать «золотую спираль», как максимально прекрасную форму в нашей Вселенной.

Золотая спираль

Чтобы максимально легко и точно построить «золотую спираль, сначала нужно построить» золотой треугольник». Любой «золотой прямоугольник» может быть поделен так, что в итоге получится квадрат и другой «золотой прямоугольник» меньшего масштаба. Теоретически это идеальное деление на квадрат и «золотой прямоугольник» может продолжаться в плоть до бесконечности. Полученные в результате квадраты как бы закручиваются по спирали, для удобства мы обозначили каждый квадрат буквами A, B, C, D, E, F и C.

(Рис.3.6)

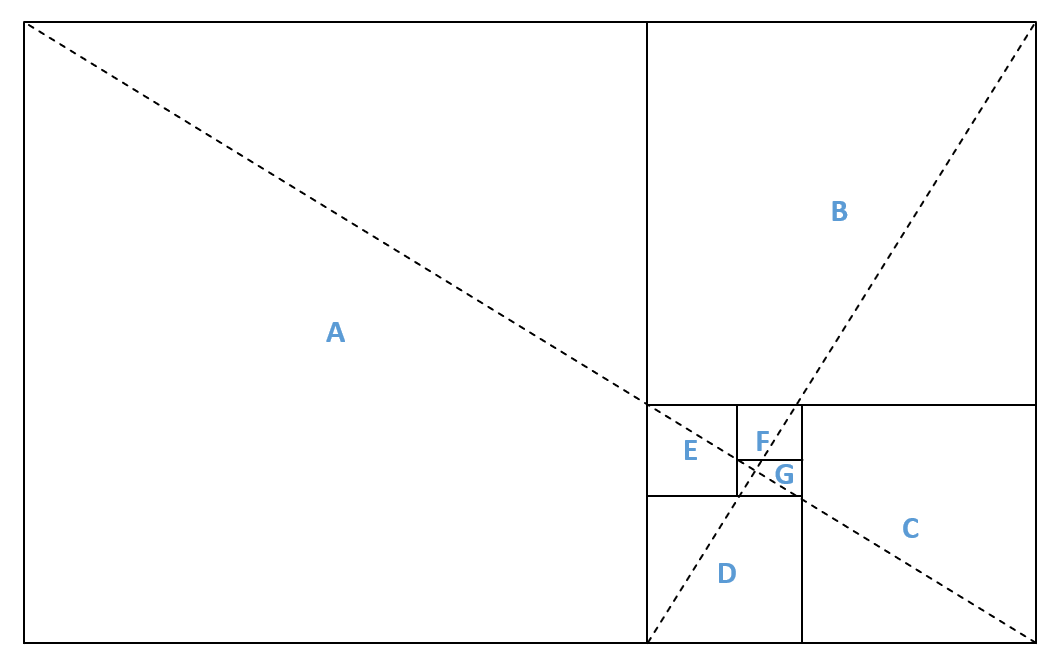
Если в получившихся двух «золотых прямоугольниках» провести отрезки по диагонали, которые сами бы имели золотое отношение друг к другу, то данные отрезки могут показывать на вероятную центровую точку закручивающихся квадратов. Чтобы начать рисовать спираль, можно ориентироваться на теоретический центр закручивающихся квадратов, нужно будет лишь соединять дугой точки пересечения всех получившихся закручивающихся квадратов и придерживаться масштаба на увеличения. Теоретические точки соединения закручивающихся внутрь и наружу квадратов показывают путь для формирования «золотой спирали».

(Рис.3.7)

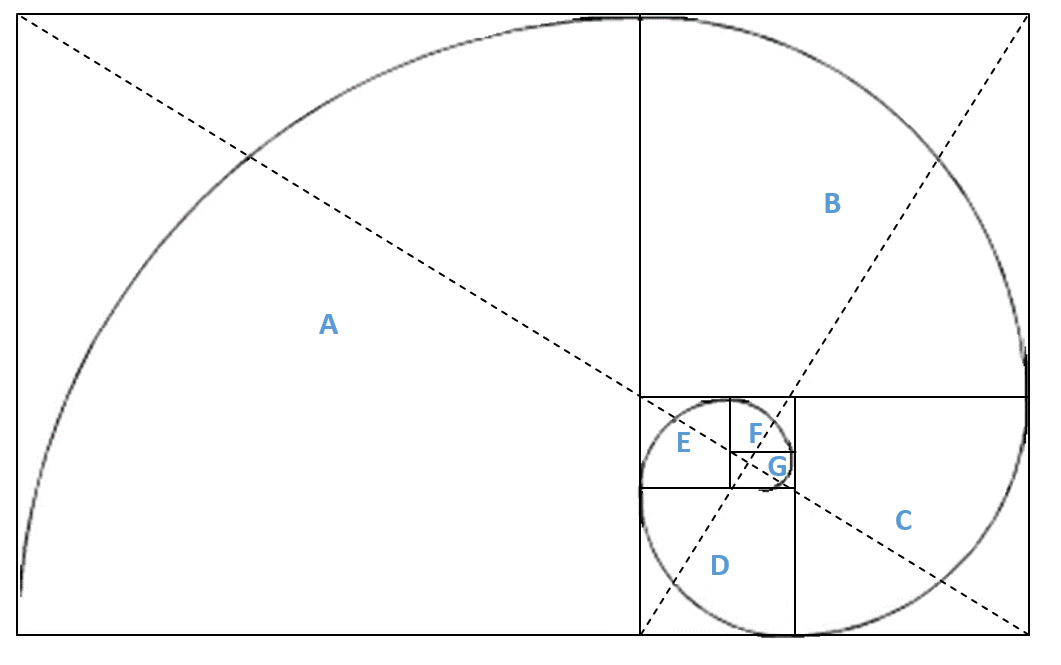
Если вы возьмете абсолютно любую точку на «золотой спирали», то вы сможете увидеть, что отношение длины дуги к ее диаметру будет стремиться к равенству 1,618. И также отношение диаметров и радиусов, отстоящих друг от друга на 90 градусов, тоже будет стремиться к значению 1,618.

(Рис.3.8)

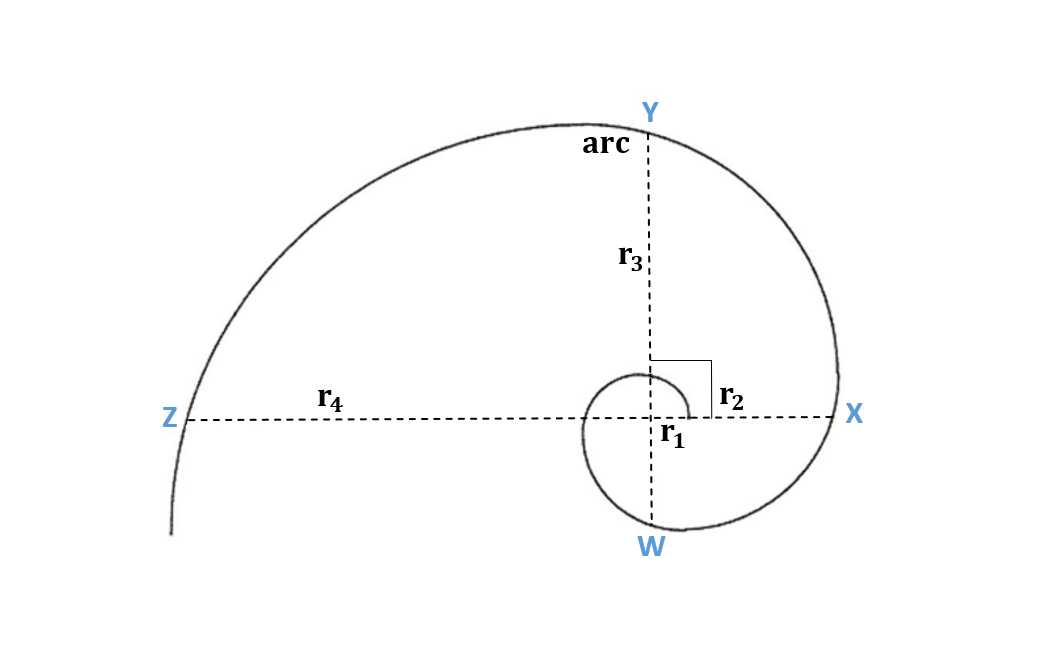
Также есть интересное наблюдение о «золотой спирали». Если «золотая спираль» является логарифмической спиралью или равноугольной спиралью, то она не имеет четких границ, но обладает при этом четкой формой. Такие виды спирали могут бесконечно самовоспроизводиться и внутрь, и наружу. Центр никогда не появляется и наружу спираль самовоспроизводиться бесконечно. Если взять логарифмическую спираль и посмотреть на нее под микроскопом, то мы увидим тоже самое если бы мы смогли посмотреть на такую спираль с расстояния в сотню световых лет.

Практически все фигуры в классической Евклидовой геометрии, кроме только эллипса, в большем своем проявлении подразумевают статичность, но не спираль. Она как не странно, содержит «движение»: она растет и уменьшается, она развертывается и сжимается, она может прогрессировать и регрессировать. Ученные везде во Вселенной находят то, что, логарифмическая спираль оказывается существенным выражением явления естественного роста. Даже такие незначительные по своему масштабу частицы как атомарные и такие гигантские как движения целых галактик придерживаются ее.

Девид Бергамини в своей работе «Математика» замечает, что движение хвоста кометы имеет изгиб в сторону от Солнца именно по логарифмической спирали. Биологи и ученные выяснили, что простейшие бактерии растут с таким ускорением, график которого имеет вид логарифмической спирали. Если взять точный микроскоп, например электронный, то можно заметить при рассмотрении искусственно выращенных кристаллов, логарифмические спирали. Такие часто встречающиеся в природе для человека вещи как еловые шишки, раковины моллюсков и улиток, морские коньки, морские волны, листья папоротников, рога млекопитающих, формирование семечек в подсолнухе, семечки в цветке маргаритки – все это формируется, образуя логарифмические спирали. Даже такие сложные природные явления как ураганы и водовороты формируются в логарифмическую спираль. И даже галактики внешнего космоса закручиваются в такую форму как логарифмическая спираль. Если посмотреть на человеческий палец, то можно увидеть, что он состоит из трех костей, отношение одной кости к другой имеют в своем составе правило «золотого сечения», и оно принимает форму спирали в согнутом состоянии. В природе мы видим проявление этого космического правила в различных формах. Если взять два таких не связанных между собой «предмета» как еловая шишка и спираль Млечного Пути (которых разделяют миллионы световых лет), то мы заметим сходство в их формировании, их объединяет коэффициент 1,618. Этот коэффициент считается первичным законом, который управляет динамикой естественных явлений. Существование «золотой спирали» — это знак и символ самого великого замысла природы. «золотая спираль» есть также символ бесконечного расширения и сжатия. Она показывает статичный закон, который управляет быстро развивающимися процессами и который основан на коэффициенте 1,618 – коэффициенте «золотой середины».

Значение числа φ

Во все просвещенные времена самые образованные люди своих поколений уделяли колоссальное внимание значению числа φ и оценивали его по достоинству. В истории сохранилось много упоминаний об умнейших людях, которые были «без ума» от значения числа φ. Одним из таких людей был Пифагор, искал для себя символ порядка и гармонии и выбрал знак пятиконечной звезды для этой цели, в котором все линии находятся в золотом соотношении касаемо других линий. Другой пример это один из известнейших математиков, который жил в семнадцатом веке, его звали Якоб Бернулли, он завещал, чтобы на его могильном камне была нарисована. А сам Исаак Ньютон почивал на кровати, на которой была выбита все та же «золотая спираль», кстати кровать известного ученного сейчас принадлежит одному из фондов в Новом Бостоне и ее можно увидеть на различных выставках.

Ученые считают, что первыми поклонниками «золотой спирали» были архитекторы и строители пирамид в Гезе, а это происходило более пяти тысяч лет назад. Они первые кто зафиксировал свое знание и отношение к значению числа φ. Ученные доказали, что древнеегипетские инженеры, архитекторы и строители осознанно использовали «золотое отношение», «золотое сечение», «золотой прямоугольник» и «золотую спираль» конструируя и возводя Великую Пирамиду. Они целенаправленно придавали ее лицевым сторонам наклонную высоту, равную половине длины ее основания помноженную на коэффициент 1,618. Именно поэтому вертикальная высота Великой Пирамиды равняется квадратному корню из произведения половины ее основания на 1,618.  Уже ранее упомянутый Питер Томпкинс в своей работе «Секреты Великой Пирамиды» произнес, что данное соотношение по-настоящему подтверждает достоверность высказывания Геродота, а именно то, что квадрат высоты пирамиды равен √ φ* √ φ = φ, а сама площадь ее измеренных фасадов равна       1 * φ = φ. Зная такие пропорции и соотношения математики вместе со строителями и архитекторами скорее всего знали такие величины как π и φ. Это им нужно было, чтобы уметь рассчитывать квадратуру круга и кубатуры сферы, а проще говоря уметь строить такой круг, чтобы его площадь была равна площади квадрата, и уметь строить такой куб, чтобы он был равный по объему сферы.

Не стоит заблуждаться на счет Великой Пирамиды и считать, что древние египтяне могли не знать всех основ «золотого сечения», хотя это и может быть правдой. Но не стоит точно забывать о том, что «золотое сечение» и ее форма во многих своих проявлениях, показывает «идеальность» для человеческих глаз и под это обаяние попадались множество величайших ученых всех времен, а вместе с ними и математики и философы и архитекторы и строители и художники. Самые ярые поклонники «золотого сечения» были Платон, Пифагор, Бернулли, Кеплер, да Винчи и Ньютон. И строители, и архитекторы той самой Великой Пирамиды тоже были гениальными учеными, астрономами, математиками и инженерами. Они может быть и не до конца понимали всех правил «золотого сечения» но точно хотели сохранить это на многие тысячелетия, думаю и считая, что это что-то очень ценное и важное. То, что такие гении мира считали важным правило «золотого сечения», говорит само за себя. А вот для чего была построена Великая Пирамида мы точно не знаем. Ученные могут только выдвигать свои гипотезы и предположения. Все гипотезы, даже самые маловероятные складываются из собственных наблюдений ученых. Самая популярная гипотеза утверждает, что Великая Пирамида — это храм, который действовал несколько веков после того, как пирамиду закончили строить. Этот храм могли посещать только избранные, те кто смогли доказать свое уникальное право на то, чтобы прикоснуться к загадкам мироздания. Только избранные могли осознать и принять вещи не такими какими они кажутся, а осознать, что эти вещи представляют собой на самом деле. И вот такие избранные люди могли посещать «мистерии», на которых рассказывались и узнавались тайны мироздания.

Интересно, а знали ли избранные люди, которые были посвящены в тайны мироздания, о существовании числа «φ»? «Фараоны Египта и жрецы считали число «φ» как некий символ, который обозначает бесконечную вечную последовательность, для посвящённых в тайны жителей Египта, этот символ был как «жизненный огонь, разум, Логос, Слово, которое упоминается в Евангелии от Иоанна» — вот что говорит нам про число «φ» Томпкинс. Логос является древнегреческим словом, которое имеет разные значения. Гераклит и так же другие языческие, европейские и христианские мыслители говорили о нем как о законе природы, как о силе, которая все создает, и которая спрятана внутри вещей, как о некой силе, которая на самом деле управляет всем миром и находится везде.

Чтобы легче понять эти слова, нужно осознать, что люди в те времена не обладали такими глубокими знаниями и не имели серьезного оборудования, для того чтобы узнать и подтвердить все то, что они не видят, а только чувствуют и предполагают. Конечно же они не знали про волновой принцип, они не чертили сложных графиков. Они не могли научно доказать и определить природные законы роста. Но имея свои знания, они делали все что от них зависело, чтобы узнать и оставить предкам понимания принципа создания природного мира, который они могли различать. Древние мыслители Египта считали и были в этом правы, что так называемая конструктивная универсальная сила правит миром и находится везде. И они также думали, а может ли эта сила править еще и в человеческом мире? Везде в нашей Вселенной встречается проявление силы числа φ. И как мы уже говорили, что все наше тело в том числе сам мозг и строение ДНК, сформировались под воздействием магии от числа φ. А что, если и сама жизнь и все что делает человек тоже формируется под воздействием этой магии? Число φ есть закон и есть импульсная сила Вселенной. Так почему же магия числа φ не может быть и движущей силой, которой бы подчинялось все в жизни человека? Может наше магическое число φ управляет всеми действиями человечества, особенно творческими процессами?  Сам прогресс человечества опирается на самовоспроизведение бесконечного ряда чисел. А может прогресс и построен на магии символа числа φ, может прогресс имеет форму спирали? Если наблюдать за фондовым рынком, а именно за прогрессом возможностей производств, то можно заметить магию числа φ. Ученые полагают, что образованные жители древнего Египта, знали, что есть нечто не видимое их взору, и это нечто имеет прямое отношение к движущей силе Вселенной. В 80 годах прошлого века теория хаоса вспомнила эту идею умных египтян. И это может быть применено и к фондовому рынку, который нужно понимать таким каков он есть, а не таким каков он кажется неокрепшим умам. Фондовый рынок — это не случайное и не хаотичное движение цен, которое происходит из-за новостей, как считают многие. Фондовый рынок — это очень точная картина формирования человеческого промышленного развития.

Вильям Кингсланд в своем произведении «Великая Пирамида в фактах и теориях» выдвигает необычное предположение. Астроном считает, что египетские мыслители и астрологи имели особый способ восприятия реальности, а именно изотерический, который был связан с циклами человеческой эволюции. А волновой Принцип Эллиотта как раз и показывает нам большие циклы эволюции человека и объясняет их появление и их действия. А еще волновой принцип работает и на огромных масштабах, и на самых маленьких. И он строится на парадоксальном принципе динамизма и вариативности внутри одной формы, которая остается неизменой.

По мнению ученных именно принцип динамизма и вариативности делает Вселенную конструктивной и придает ей единство. Ни одна вещь в природе и во Вселенной не является неупорядоченной или бесформенной. Все верно с точностью до наоборот.

Интересно что в английском языке слово «Вселенная» имеет обозначения «единого порядка». Если мы говорим о том, что у всего живого есть определенная форма строения, то мы не можем тоже самое не сказать о том, что человеческий прогресс хаотичен. Это не так, человеческий прогресс — это часть жизни человека, часть его реальности и эта часть имеет определенную форму и следует определенным правилам порядка и формирования. Из этого заключения мы можем сделать вывод, что и фондовый рынок, который как раз и показывает динамику промышленного развития человечества тоже имеет определенную форму и порядок. Все технические анализы на фондовом рынке состоят из четких правил и порядков, которые анализируют именно форму графиков и порядок изменения цен. А вот Волновой Принцип Эллиотта более глубоко смотрит на это. Принцип говорит нам о том, что не так важна сама форма и ее масштаб, самое главное то, что строение формы всегда является неизменной конструкцией.

Эллиотт пошел еще дальше. Он называл свою теорию «Волновым принципом», а также имел и второе название «Закон природы – Тайны мироздания». И свою теорию он использовал не только для аналитики фондового рынка, но применял ее для всех видов человеческой деятельности. Да, слова Эллиотта, о том, что его теория и есть главная тайна мироздания, слишком эмоциональные. Природа, создавая множество форм, процессов и правил творила не просто одну неизменную форму. Тем не менее многие современные ученые согласны с таким определением Эллиотта. Мы бы его перефразировали и сказали, что волновой принцип является одной из наиболее важных тайн природы.

Фибоначчи и спираль фондового рынка

Верно ли утверждение, что фондовый рынок подчиняется таким же математическим правилам каким подчиняется весь природный мир? Мы считаем, что такое утверждение верно. В своей работе Эллиотт говорит нам, что все ценовые движения на фондовом рынке формируются, опираясь на правила и законы, которыми управляет порядок мироздания. Закономерность Фибоначчи контролирует количество волн, которые развиваются, основываясь на движении различных индексов на рынке, и получается соотношение волн пять к трем.

В момент формирования рынок показывает нам целую закономерность Фибоначчи. Рост состоит из пяти волн и чаще всего является импульсом. Далее следует коррекция, которая чаще всего состоит из трех волн. Рост является прямолинейным подъемом. Коррекция выражается прямолинейным снижением. А сам цикл состоит из двух линей. Это первый уровень сложности в формировании структуры рынка.

(Рис.1.4)

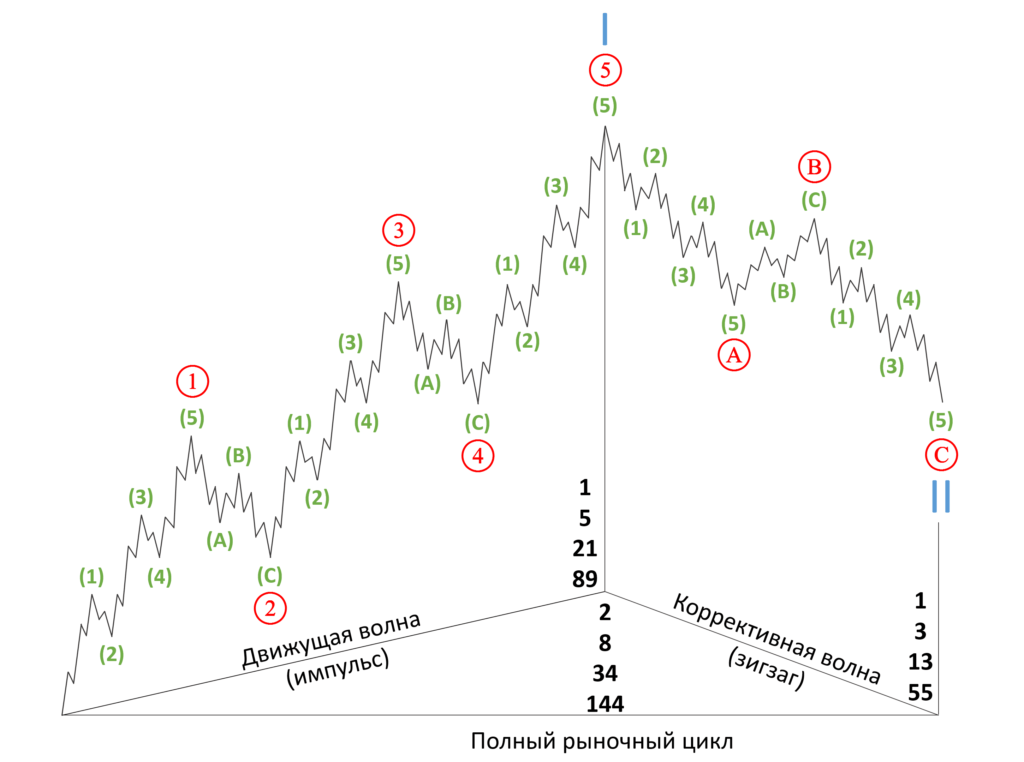
Далее формируется следующий уровень сложности и появляются числа три, пять и восемь (данная цифровая последовательность является бесконечной). И мы можем сделать вывод, что волны на финансовых рынках показывают нам ряд чисел из последовательности Фибоначчи, а значит, что мысли и эмоции массы людей магическим образом связаны с математической последовательностью Фибоначчи.

(Рис.3.10)

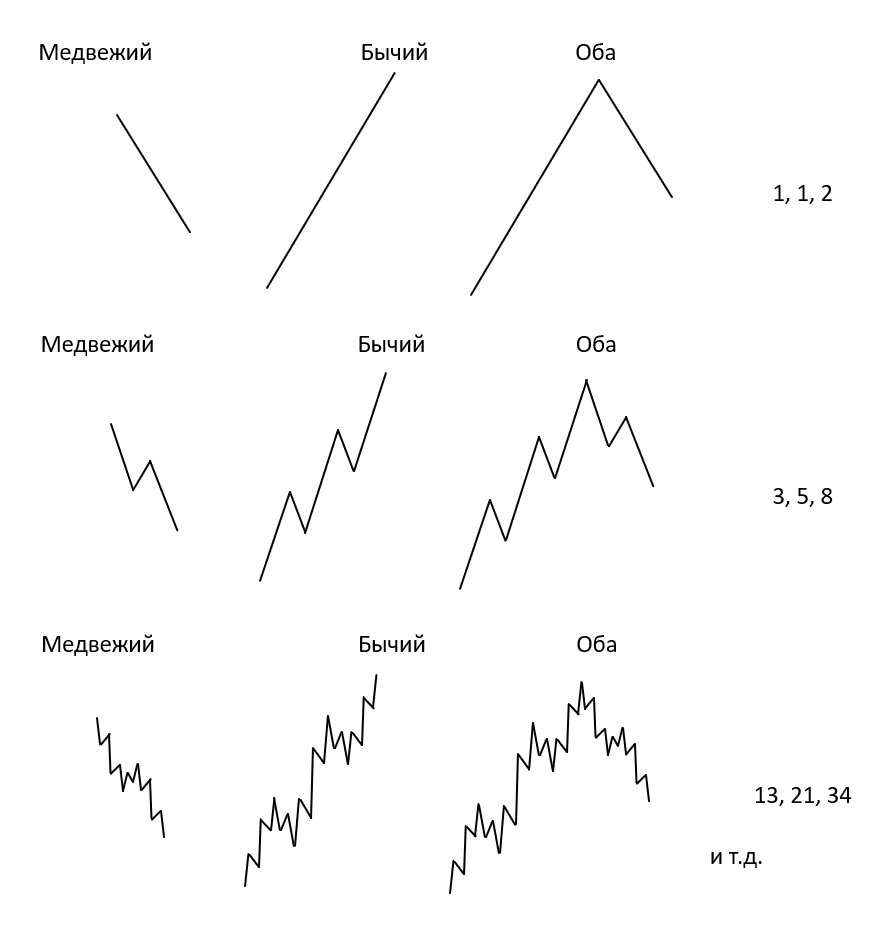
Обратите внимание на два изображения, которые приведены ниже (рис. 3-11 и рис. 3-12). На этих двух изображениях нам показывается два разных графика на финансовых рынках, и в первом, и во втором случае мы видим проявления закона природы, а именно формирование обоих графиков направленно внутри золотой спирали и это все формируется благодаря числовой последовательности Фибоначчи. Если посчитать числовое значения соотношения одной волны к предыдущей, то мы увидим, что оно будет равно 0,618 и это верно для всех волн в обоих графиках. Все числовые значения на обоих графиках выражены в пунктах и так же сами расстояния показывают нам проявления закона Фибоначчи.

(Рис.3.11)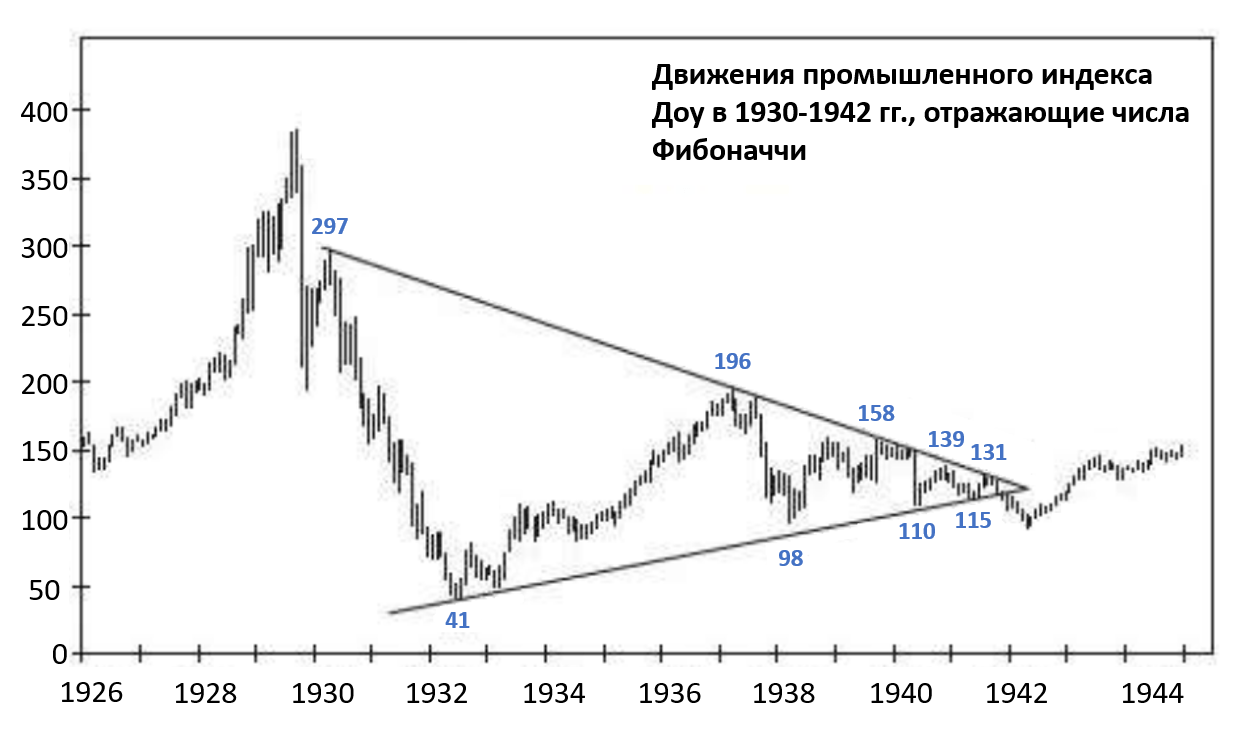

 

(Рис.3.12)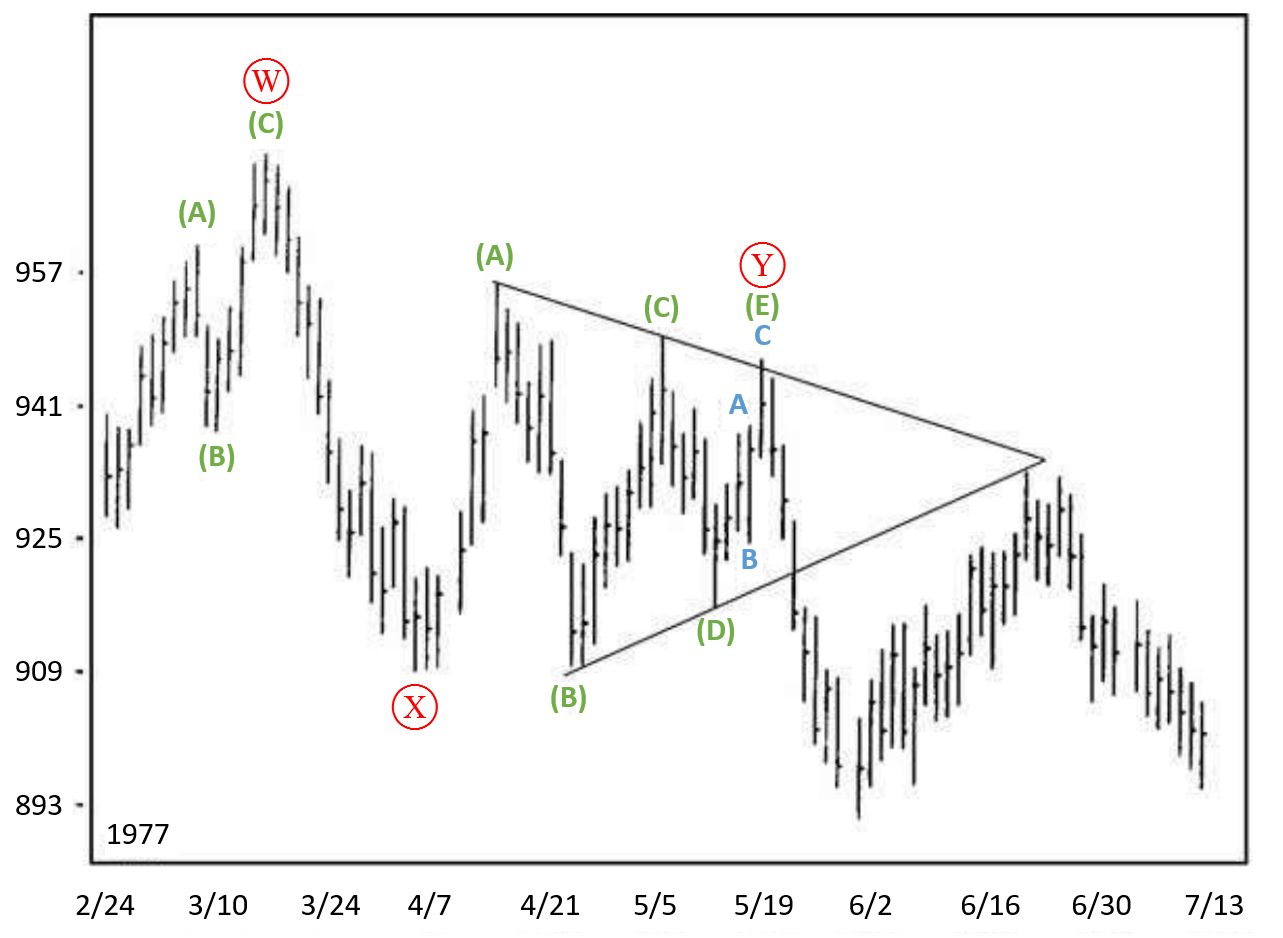

Посмотрите на иллюстрацию 3-11 и на отрезок графика начиная с 1930 года и заканчивая 1942 годом. Нам показана числовая закономерность, при которой рынок колеблется и покрывает примерно 260, 160, 100, 60 и 38 пунктов Доу. И данная последовательность очень схожа к уменьшающемуся списку коэффициентов Фибоначчи (2,618; 1,618; 1,00; 0,618; 0,382).

Теперь посмотрите на иллюстрацию 3-12, а именно на отрезок графика, начинающийся с волны [Х]. Мы видим коррекцию, которая направлена вверх и в данном случае колебания цен равны 55 пунктам Доу (сама волна [Х]). Волна (A) равна 34 пунктам Доу такое же значение имеет и волна (C); волна (D) равна 21 пунктам Доу; волна A of (E) равна 13 пунктам; волна B of (E) равна 8 пунктам. Данный ряд является последовательностью Фибоначчи. Также интересно следующее наблюдение: рост от начала и до конца на разбираемой части графика равен 13 пунктам Доу, а сама вершина треугольника данного отрезка находится на уровне начала коррекции 930 пунктов Доу, а это в свою очередь есть уровень пика нового роста цен в июне. Если бы данное соотношение появлялось не так часто, то мы бы могли говорить, что это всего лишь совпадение. Но такое соотношение между волнами появляется постоянно и при этом в большинстве случаев оно равно 0,618, а э то уже точно не может быть просто совпадением.

Можно ли утверждать, что формирование на финансовых рынках формируется благодаря законам Фибоначчи и отражает спиральный рост? Мы считаем, что и это утверждение является верным. Посмотрите на рисунок, изображенный ниже. Он как раз показывает схематично, что формирование движения на финансовых рынках опирается на волновую теорию Эллиотта и это в свою очередь может являться прекрасной основой для того, чтобы начертить логарифмическую спираль, опираясь на движения фондовых рынков. В этом схематическом примере вершина каждой волны роста на степень выше и есть точка, через которую проходит экспоненциальное расширение.

(Рис.3.13)

Мы коснулись двух главных способов оценки в промышленной жизнедеятельности человека с социологической точки зрения, а именно рассмотрели последовательность Фибоначчи и спиральное развитие. Эти два способа показывают и остальные формы роста, которые можно найти в природе. И поэтому мы можем утверждать, что все они подчиняются одним и тем же законам.

Математика Фибоначчи в структуре волнового принципа

Как уже было несколько раз сказано, волновая теория Эллиотта построена на принципах, которые имеются в последовательности Фибоначчи. В волновой теории есть главная форма волн, которая представлена пяти волновой структурой. Также есть два типа волн первый это движущиеся волны, которые на графиках обозначаются цифрами, второй тип волн это коррекционные, они на графиках обозначаются буквами. Также есть три группы волновых моделей: пятерки, тройки и треугольники, последние обладают характеристиками и троек, и пятерок. Есть пять семейств: импульсы; диагонали (начальная диагональ и конечная диагональ), зигзаги (простые зигзаги, двойные зигзаги; также Эллиотт выделяет тройные зигзаги, но так как этой моделью можно разметить почти любой участок, она становится бессмысленной для прогнозирования, поэтому мы ее не используем, и в 99% случаях участок, который кажется, что представлен только тройным зигзагом можно разметить альтернативно),  плоскости (бегущая, расширяющаяся, нормальная), треугольник (сходящиеся треугольники делятся на два типа нормальный и бегущий, также Эллиотт выделяет расходящиеся треугольники, но команда Пректера нашла только два примера таких моделей за все время их аналитики, а это значит, что статистики поведения по данным моделям нет, и их прогнозирование бессмысленно, и также наша команда волновиков смогла альтернативно разметить данные два примера, где команда Пректера показывает расширяющиеся треугольники, поэтому мы не используем эту модель для аналитики). И получается, что существуют тринадцать моделей в волновой теории Эллиотта: импульсы, начальная диагональ, конечная диагональ, одинарный зигзаг, двойной зигзаг, бегущая плоскость, расширяющаяся плоскость, нормальная плоскость, сужающийся симметричный треугольник, сужающийся нисходящий треугольник, сужающийся восходящий треугольник – эти одиннадцать моделей мы используем в своей аналитики; тройной зигзаг и расширяющийся треугольник мы не используем.

В волнах коррекции команда Пректера насчитывает две группы коррекций, а именно простые и комбинированные, и это уже получается 3 группы (движущиеся, простые коррективные, комбинированные коррекции).  Различаются два вида классов в комбинированных коррекциях (в комбинациях), а именно двойные коррекции и тройные коррекции, и получается, что всего классов пять. Команда Пректера считает, что в комбинациях может быть только один треугольник и один зигзаг, и получается 8 семейств комбинаций, а вместе с импульсом, диагональю, плоскостью и треугольником получается тринадцать семейств, и если считать все простые модели и все модели в семье комбинаций, то получится двадцать одна модель. Мы же в своей аналитики придерживаемся мнения, что в комбинации может быть только пять моделей. А какие это именно модели Вы можете узнать, придя к нам на обучение.

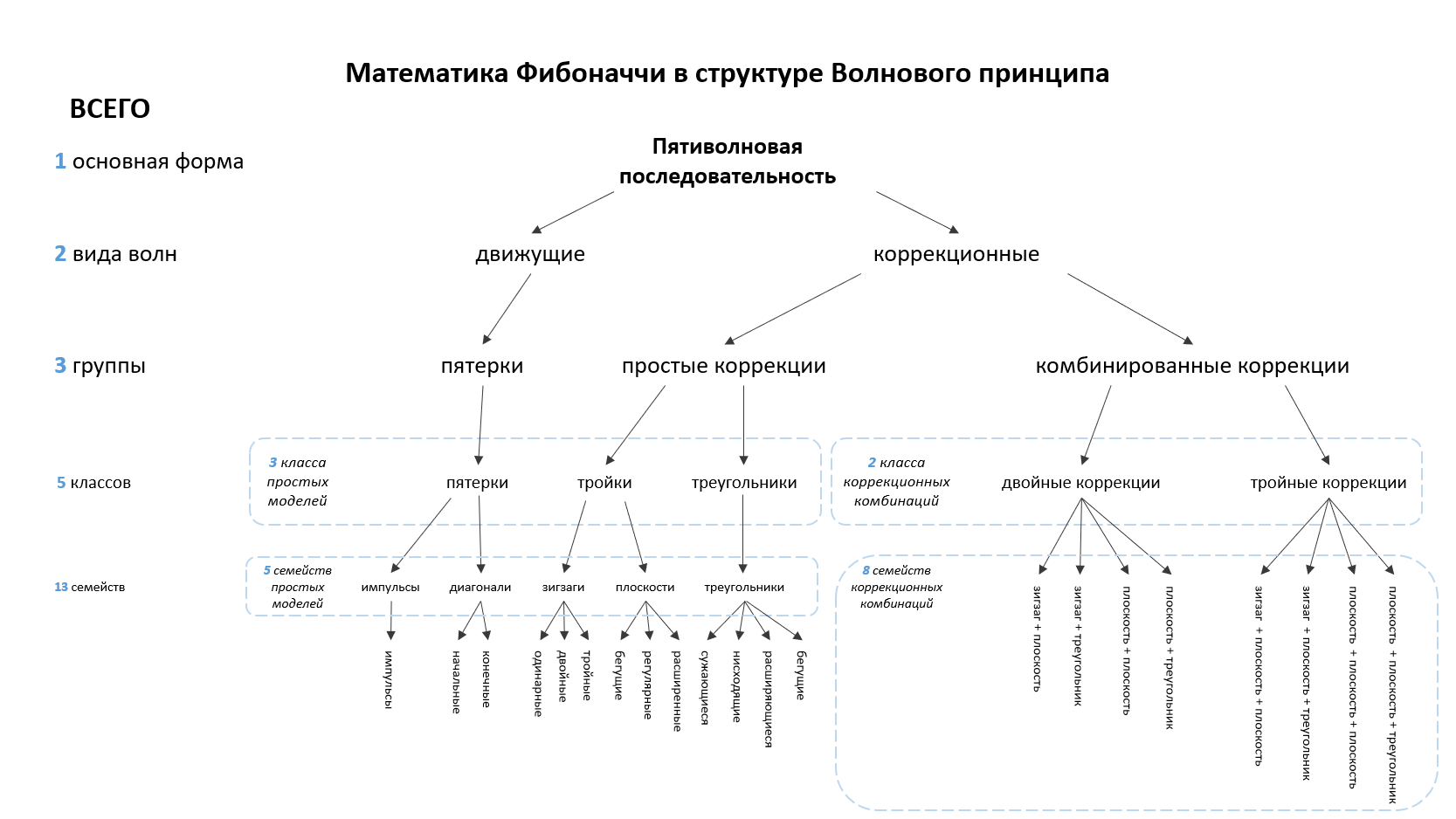
На рисунке, который представлен ниже, вы можете увидеть все имеющиеся модели по Пректеру, это называется древо развития строения сложной волновой модели, которое отражает законы последовательности Фибоначчи. Также на рисунке указаны перестановки в комбинациях и также последовательность в вариативности меньшей важности внутри волн. Например, мы можем понять какая из волн может быть растянута, если, конечно, растяжение имеет место быть; как именно строится чередование волн, может ли импульс иметь в своей структуре диагональ, чем может является комбинация и так далее. Эта схема может помочь начинающему волновику в его первых аналитических разметках.

Благодаря этой классификации, волновик может применять свойство вариативности волн, главное не делать этот процесс надуманным, ведь начинающий волновик может увидеть возможные вариативные модели, которых нет на самом деле, смотря на данную классификацию. Но это не так значимо, главное то, что мы видим, как формируется данное строение волновых моделей и замечаем, что это строение имеет в себе законы Фибоначчи.

(Рис.3.14)

Число φ и аддитивный рост

При углубленном изучении фондового рынка и волновой теории Эллиотта можно обнаружить, что рынок следует по правилам золотого соотношения, а последовательность Фибоначчи на фондовых рынках можно увидеть так часто, что это уже нельзя назвать чисто случайностью. Но новичку волновику нужно помнить, что и правила золотого отношения и последовательность Фибоначчи, как и в жизни так и на финансовых рынках так и в волновом методе, все-таки имеют теоретическое значение, а вот соотношения этих теоретических закономерностей и есть тот самый грааль и ключ к пониманию фондового рынка. Команда Пректера и сам Эллиотт не редко говорили, что последовательность Фибоначчи встречается в аддитивной последовательности и не имеет значения с каких именно чисел начинается эта самая последовательность. Саму закономерность Фибоначчи можно назвать базовой аддитивной последовательностью, ведь она формируется с числа один, а сама по себе цифра один есть начальная точка в математическом росте.

(Рис.3.15)

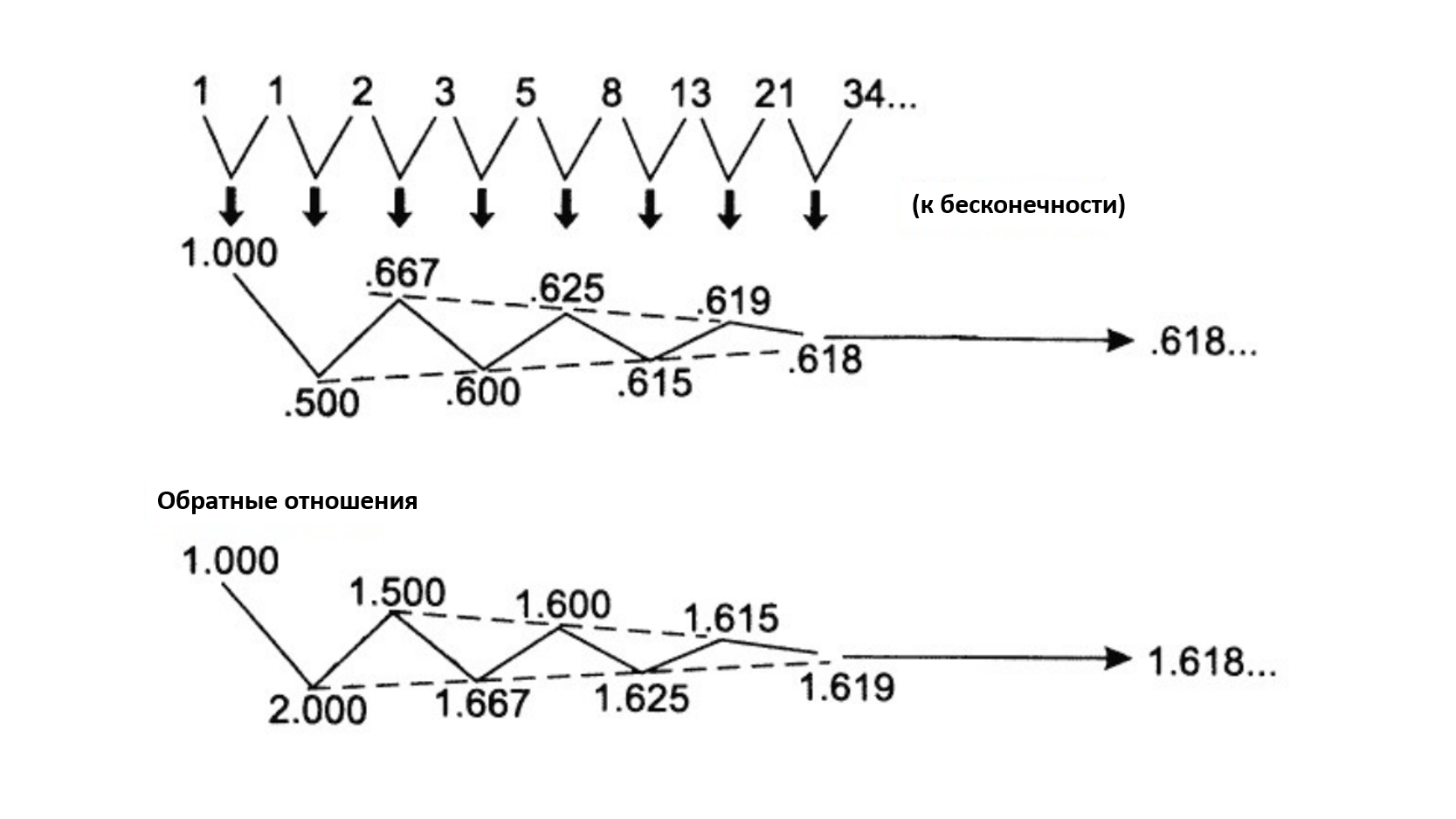
При этом любой человек если выберет два любых числа и сложит их вместе и получит третье число. А по мере увеличения этой прогрессии взаимоотношения соседних чисел в закономерности чаще всего быстро стремится к значению равному φ, а когда появляется восьмой член эта последовательность становится очевидной.

(Рис.3.16)

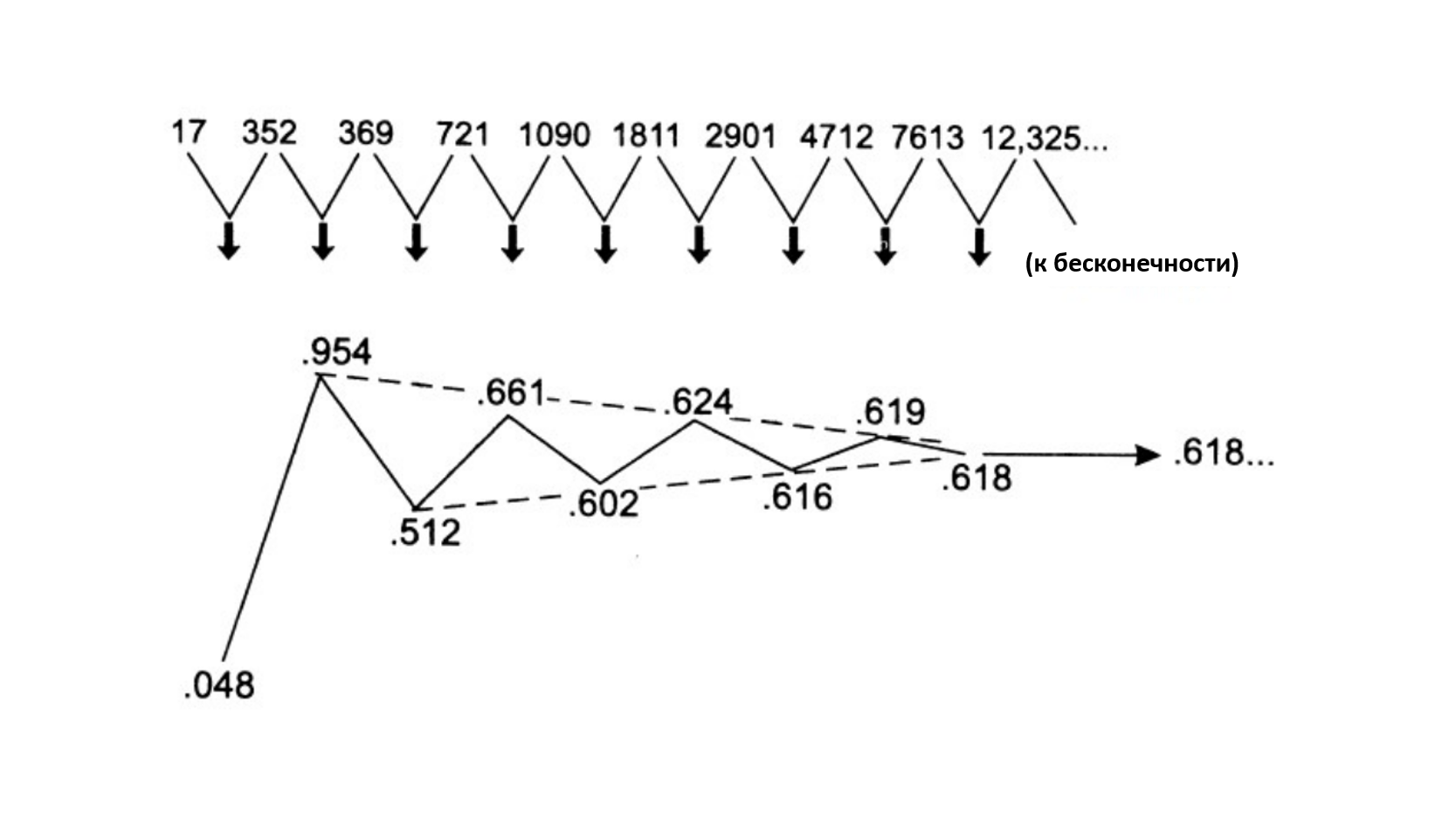
Получается, что некие определенные значения, которые формируют закономерность Фибоначчи показывают идеальную волновую прогрессию, которая появляется на финансовых рынках, а коэффициент последовательности Фибоначчи и есть главный закон прогрессии, и в нем два предыдущих числа можно сложить и получить следующее число. Именно поэтому коэффициент Фибоначчи может влиять и контролировать огромное число отношений в рядах данных, которые связаны с природными явлениями роста и падения, расширения и сужения, подъёмов и снижения.

Поэтому волновая теория Эллиотта говори нам о том, что законам и принципам, которые воспроизводят живые существа и целые галактики, свойственен дух и людской деятельности. А мы же знаем, что фондовый рынок отражает сентимент психологии масс и поэтому, анализируя этот достоверный барометр можно увидеть точную картину и социального и психологического состояния людей и их склонности. Именно эта картина изменяющейся характеристики промышленной деятельности показывает себя в некоторых моделях прогрессии и регрессии.

Волновая теория Эллиотта показывает нам, что формирования промышленной деятельности человека (ее мы как раз и можем оценить, анализируя финансовые рынки) не формируется в виде прямой линии, и не является случайным движением или случайным циклом. А развитие промышленной жизни человека «делает три шага вперед и два назад», или «пять шагов вперед и три шага назад», как сказали бы настоящие волновики, ведь промышленная и социальная жизнь людей формируется под действием закономерности Фибоначчи, а также основана на принципах спиральной модели развития, и может даже придерживается правил вселенского закона упорядоченного роста.

По мнению команды Пректера, слишком много взаимосвязи между волновой теорией Эллиотта и другими природными явлениями и законами. И эти взаимосвязи слишком явно выражены, поэтому ими нельзя пренебрегать. Именно поэтому команда Пректера, принимая во внимание принципы вероятности, выдвинула свое мнение о том, что есть некий «вездесущий» принцип, который создает все социальные и промышленные явления, и именно поэтому сам Эйнштейн любил повторят, что «Бог не играет в кости со Вселенной». И финансовые рынки следуют этой цитате, ведь поведения масс, точно связанно с законами, которые можно проанализировать, изучить и определить. А самый простой пример, который это подтверждает, является коэффициент 1,618.

Человеческая жизнь формируется, следуя неким законам? Мы считаем, что точно да! Эти самые законы применимы и для всех финансовых рынков? Мы считаем, что точно да! Поэтому и работает волновой принцип Эллиотта? Точно да! Именно это, имел в виду поэт Макс Эрманн говоря, что: «Ты Вселенной дитя, как деревья и звезды. Это место по праву твое. Думай, что хочешь, а мир вращенья проходит своим чередом».